Lav et ægyptisk kvadrat

Kort om forløbet
Mål et kvadrat op på jorden på 7 x 7 meter - ved hjælp af snore og pløkker, som de ægyptisk landmålere gjorder.
Geometrien opstod som en følge af landbruget i det gamle Ægypten og Mesopotamien (det nuværende Irak).Landbrugsarealer skulle måles ved salg, arv og skattebetaling.
Datidens landinspektører og landmålere måtte betjene sig af simple redskaber for at kunne løse deres opgaver. De skulle måle længder uden at have målebånd, som i dag kan købes i ethvert byggemarked. De måtte bruge særlige metoder til at lave rette vinkler. Dem skal vi også arbejde med i denne opgave.
Formål
Formålet med forløbet er at eleverne
- arbejder undersøgende med kvadratet i praksis
- beskriver et kvadrat
-
får en fornemmelse af hvor svært det er at opmåle rette vinkler.
Forberedelse
Sådan gør du
Opgaven går ud på at lave et kvadrat på samme måde, som de gamle ægyptere gjorde, når de skulle lave fundamentet til en bygning. Du skal lave et kvadrat, som er 7 x 7 meter.
Del eleverne op i grupper på 2 - 4. Hver gruppe kan starte med at snitte en meterstok og 7 – 8 pløkke af grene de finder på jorden. Giv hver gruppe et ark, som beskriver fremgangsmåden:
Fremgangsmåde
Fremgangsmåden indeholder 5 trin.
TRIN 1: Basislinie
Du skal først lave en basislinie. Den behøver ikke at have et præcist mål – men gerne mellem 5 og 8 meter.
I hver ende af basislinien sætter du en pind i jorden. Gerne en lidt tyk pind, som du kan få til at sidde godt fast (evt. ved at tage en sten og slå den ned som en pløk).
Du tager snor nr 1 forbinder de to pinde. Det er din basislinie – som går fra punkt A til punkt B.

Basislinjen AB
TRIN 2: Lav en vinkelret linie
Du tager nu snor nr. 2 og binder en lille pind P fast nogenlunde på midten af snoren. Når det er gjort, binder du enderne på snoren fast til A og B.
Når det er gjort – trækker du snoren med den lille pind ud, så den danner en trekant med basislinien. Dér, hvor den lille pind er, sætter du en anden pind, som du kalder M.
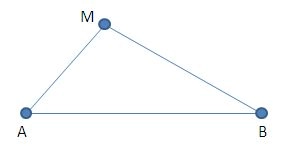
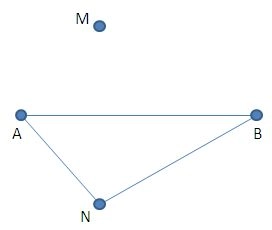
Nu fjerner du snor nr. 2 fra A og B – og du fjerner den lille pind P fra snor 2. Så står der kun fire pinde tilbage – A, B, M og N. Snor 1 forbinder stadig A og B.
Herefter forbinder du M og N vha. snor 2 – og dér hvor snor 1 og snor 2 krydser hinanden, sætter du en pind, som du kalder X. X bliver det ene hjørne i det kvadrat, som du skal lave.
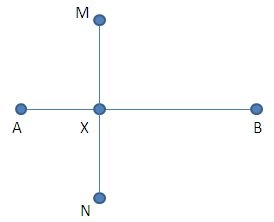
TRIN 3: Lav siden XY
Tag snor nr. 3 og bind knuder på den for hver meter (du har meterstokken til hjælp). Der skal være 8 knuder på snoren for at du kan måle 7 meter.
Anbring den første knude ved X og træk snor nr. 3 ud, så den flugter med B. Sæt en pind Y ved den sidste knude (den 8. knude). Nu er afstanden mellem X og Y 7 meter. Y bliver det andet hjørne i det kvadrat, som du skal lave.
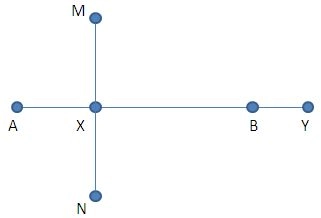
TRIN 4: Lav siden XZ
Anbring den første knude ved X og træk snor nr. 3 ud, så den flugter med M. Sæt en pind Z ved den sidste knude (den 8. Knude). Nu er afstanden mellem X og Z 7 meter. Z bliver det tredje hjørne i det kvadrat, du skal lave.
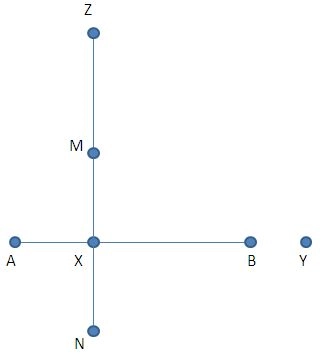
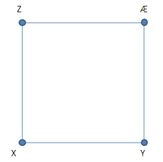
TRIN 5: Find placering af Æ
Start med at fjerne pindene A, B, M og N – og alle snore. Så ser situationen sådan ud:

Bind snor nr. 1 fast i Y og snor nr. 2 fast i Z. Bind en knude K på snor 1 og en knude L på snor 2, så KY og LZ hver er 7 meter.
Brug din snor nr. 3 med knuderne som målebånd til at lave knuderne K og L.
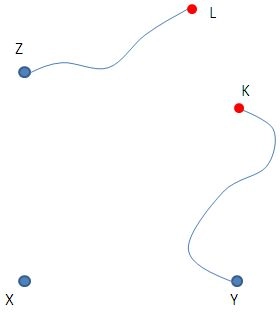
Den ene kammerat holder fast i knuden K på snor nr. 1, og den anden kammerat holder fast i knuden L på snor nr. 2.
De skal hver især stramme snoren ud og gå sammen, så de to knuder mødes. Dér hvor de to knuder mødes er punkt Æ.
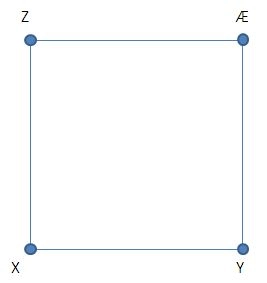
Afslutning på opgave
Blev kvadratet ”perfekt”? Hvis I har et målebånd, kan I prøve at måle afstandene af diagonalerne YZ og XÆ. De skulle gerne være lige lange – og de er et godt mål for kvaliteten af jeres arbejde.
Til sidst skal I lave en liste over, hvilke forhold, der kan give fejl eller unøjagtigheder undervejs i arbejdet med at skabe et ”perfekt” kvadrat.
Her er et par eksempler på årsager til unøjagtigheder:
- Knudernes afstand er ikke præcist en meter
- Når I flugter en snor ud fra to pinde, gør I det ikke helt præcist
Find selv mindst 3 andre årsager til unøjagtigheder.
Baggrund
Hvad er et kvadrat
Et kvadrat er en plan firkant, hvori alle sider er lige lange, og alle fire vinkler er rette (90°).
Et kvadrats størrelse angives med sidelængden s. Da kvadratets areal er lig med s², bruges ordet "kvadrat" også indenfor matematikken om et tal opløftet til 2. potens; således omtales størrelsen s² som "kvadratet på s".