Byg en bro over åen

Forberedelse
Klassen kan med fordel forinden have arbejdet med trekanter og deres vinkler samt have talt om hvordan man kan benytte ensvinklede trekanter i praksis i forbindelse med udeskole.
Vi ser det som en fordel, at den lærer som står for aktiviteten har fortalt eleverne om det område, de skal besøge, og om dettes muligheder i matematisk kontekst.
Opgaven udføres i grupper af størrelsen 2-4 personer.
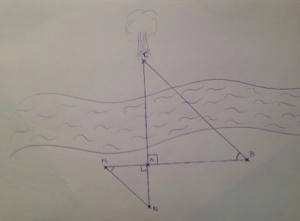
Trekant og å. Tegning: Amalie, Anne Mette og Christina.
Sådan gør du
- Find et pejlemærke på den anden side af åen/søen, der står ca. 2 meter fra vandkanten. Pejlemærket kaldes punkt C. (Pejlemærket bør være et realistisk sted for, hvor du ville anlægge en bro)
- Person 1 stiller sig direkte overfor det valgte punkt, og danner punkt A (ligeledes 2 meter fra vandkanten)
- Person 2 afsætter punkt B til højre for person 1, således at vinkel A bliver en ret vinkel.
- Der er nu en retvinklet trekant ∠CAB (se tegning).
- De to fundne punkter afmærkes, punkt A og punkt B.
- Eleverne skal nu måle afstanden |AB| = ______ som nu er trekantens grundlinje.
- Herefter måles vinkel B med vinkelmåleren.
- Vinkel C kan nu udregnes, ud fra viden omkring vinkelsummen i en trekant.
- Der skal nu dannes en ny retvinklet trekant. Grundlinien AB i trekant CAB forlænges ved at afsætte et punkt M til venstre for A. Afstanden AM er grundlinien i den nye trekant.
- Mål grundlinjen |AM| = ______
- Forlæng højden |AC| på den bred i arbejder på. Dette gøres da denne linje også skal danne højde i den nye trekant AMN
- Stil jer nu på punktet M og afsæt en vinkel af tilsvarende størrelse som vinkel B.
- Følg den linje vinklen M danner indtil denne krydser forlængelsen af linje |AC|. Her afsættes den nye trekants sidste punkt N.
- Mål herefter og noter
- |MN| = _______
- |NA|= _______
- |AM| = _______
- Find derefter forstørrelsesfaktoren, ved hjælp af linjestykke |AB| og |AM|.
- AMAB=
- Brug denne forstørrelsesfaktor til at finde de ukendte længder i trekant ABC.
Bonus opgave for de hurtige:
- Regn ud hvor mange brædder der skal bruges til at bygge en bro henover åen/søen.
- Selve skelettet for broen skal ikke medregnes, men kun brædderne der skal ligge ovenpå.
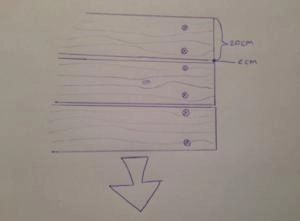
- Hvert bræt er 20 cm. bredt og der skal være 2 cm. mellemrum mellem hvert bræt.
- Hvert bræt er fæstet med 6 søm, hvor mange søm skal der benyttes til jeres bro?
Bearbejdning
Efterfølgende kan man i klasselokalet foretage en diskussion af arbejdsmetoden i plenum, samt hvordan grupperne er kommet frem til resultaterne.
Spørgmål de rkan være relevante i en plenum samtale:
- Er nogle fremgangsmåder mere hensigtsmæssige end andre?
- Kunne man være kommet frem til længden af broen vha. en anden fremgangsmetode?
- Hvilke andre steder vil det være relevant at måle brugen af denne metode?
- Hvordan kan man gøre, hvis man ikke har en retvinklet trekant?
- Deltog alle i gruppen til opgaveløsning?
- Var der noget i opgaven der var svært at forstå?
Dernæst anbefales det at træne tegning og beregning i dynamiske geometriprogrammer såsom GeoGebra.
Forslag til videre arbejde
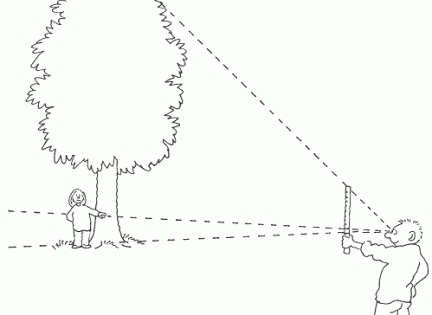
Efterfølgende arbejde kunne består i at gentage lignede opgaver med ensvinklede trekanter, der ikke havde en ret vinkel, samt at bruge ensvinklede trekanter til at måle højder, der ikke er mulige at måle fysisk, fx. et gammelt egetræ. Til dette anbefaler vi brugen af en Jakobsstav.
I kan også bygge broen over åen - i virkeligheden. Det er der også masser af matematik i.