Hvor meget træ er der i en træstak
Formål
- At gøre eleverne bevidste om at der i virkeligheden ikke findes ret mange former der passer rent ind i de geometriske former, vi kender fra klasselokalet.
- At give eleverne mulighed for at tilpasse skolens former og regneregler på en måde, så man kan måle indholdet af uregelmæssige former – det kan være træstakke - i skoven.
- At lege med begreber som rummeter og kubikmeter fastmasse
-
At bruge procentregning til at fastsætte træmassen – fastmassen – i en træstak.
Forberedelse
Rummeter og kubikmeter
Ved at måle træ i skoven der er stablet i stakke, kommer eleverne ind på begreber som:
- Rummeter træ, dvs. rumfanget af træ + luft i stakken
- Kubikmeter træ, dvs. rumfanget af rent træ i stakken
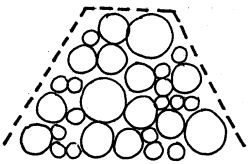
Find stakke
Kontakt den lokale skovfoged og undersøg, om der i skoven er nogle stakke af træ, som I må bruge til at måle op. Det skal ikke være nogen bestemt træart, men må gerne være stabler af forskellig størrelse og også gerne stakke med henholdsvis grantræ og løvtræ.
Det vil være en fordel, hvis du har været ude og inspicere stablerne inden klassen er med, så du er forberedt på, hvilke faktorer som har betydning for bestemmelsen af fastmassetallet.
Den bedste stabelstørrelse er under 10 rummeter. Den er rimelig overskuelig at måle op. Større stakke har dog den fordel, at de kan bringe flere aspekter og overvejelser ind i billedet.
Årstid
Forløbet kan gennemføres hele året. Der ligger træstakke i skoven året rundt. Men det er om vinteren, at det meste træ fældes, når jorden er frossen og hård at køre på. Her kan forløbet evt. suppleres af, at eleverne ser et træ blive fældet.
Forberedelse i klassen
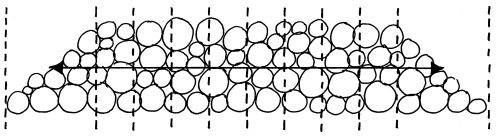
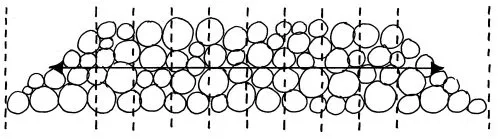
Dimensionerne i en træstak: Højden i gennemsnit. Bredden i gennemsnit.
Arbejd f.eks. med dimensionerne i en træstak:
- Højden af stablen (H):
Del stablen ind i et antal lige store sektioner (se tegning). Man vil typisk vælge 10 sektioner: 8 der er lige store og 1 i hver ende, der indbefatter hele den skrå afslutning. Vurdér gennemsnitshøjden indenfor hver sektion (h1, h2, h3…, hn). Beregn én samlet gennemsnitshøjde (H) for hele træstablen (H = h1 + h2 + h3 + … + hn / n). I princippet vil I derpå regne på arealet af et rektangel, der har samme højde som gennemsnittet af stablens mange højder.
-
Længden af stablen (L):
Enten den øverste længde + den nederste længde divideret med 2.
Eller en længde fra et vurderet midtpunkt på den ene skrå ende til en vurderet midtpunkt på den anden skrå ende (se tegning).
- Bredden af stablen (B):
Den gennemsnitlige længde af de skårne træstykker (træeffekter).
Det vil også være en fordel, hvis der er dannet faste hold, der har drøfter arbejdsfordelingen hjemmefra.
Sådan gør du
I skoven
Når I ankommer til skoven, udpeger du de forskellige stabler for de enkelte hold. Hvert hold skal herefter gennemgå følgende:
A. Stakkens rumfang i rummeter
Mål i meter:
- Højde af træstakken (H):
Del stablen ind i et antal lige store sektioner. Vælg f.eks. 10 sektioner, 8 der er lige store og én i hver ende der indbefatter hele den skrå afslutning. Bestem gennemsnitshøjden i hver sektion (h1, h2, h3,..., hn). Beregn én samlet gennemsnitshøjde (H) for hele træstablen (H = h1 + h2 + h3 + ... + hn / n). - Længde af træstakken (L):
Den gennemsnitlige længde af træstakken er afstanden mellem midten af den ene endes skrå del og midten af den anden endes skrå del. - Bredde af træstakken (B):
Den gennemsnitlige længde af træstammerne i stablen. - Rumfanget af stablen = højde x længde x bredde:
Rumfanget er i rummeter, dvs. rumfanget af både træet og den luft der er imellem træstykkerne.
B: Stakkens vedmasse
Nu skal I bestemme hvor mange kubikmeter træ (uden luft) der er i stakken. Dette tal kalder man også for vedmassen:
- Mål diameteren af hver stok (stykke træ) på hver side af stablen. Prik diameteren ind i et skema som det vist herunder. Når diametrene skal måles på begge sider er det fordi at hver stok har en tyk og en tynd ende. Måler I kun den ene sides diametre risikerer man at for en for høj eller for lille grundflade af stokkene. Diameteren måles med tommestok eller målebånd.
- Mål længden på alle tilgængelige stokke, og beregn en gennemsnitslængde. Noter denne.
- Beregne grundfladen for hver diametergruppe. En stoks grundflade beregner I ved at bruge formlen for arealet af en cirkel (A = radius2 x P) hvor P er cirka 3,14
- Læg alle grundflader sammen. Divider tallet med 2 (I har jo målt både forside og bagside af stablen).
- Gang med stammernes beregnede gennemsnitslængde, så har du stakkens vedmasse (= rumfanget af træ i stakken).
Skitse til skema
Her er en skitse til et skema til opmåling af træstak og bestemmelse af vedmasse:
| Diameter | Grundflade | Længde | Beregning | Vedmasse |
C: Stakkens fastmasse
Fastmassetallet er et udtryk for hvor mange procent træ der er i en rummeter. Beregn fastmassetallet ved at dividere vedmassen med rumfanget.
Fastmassetal = Vedmasse (m3) / Rumfang (rummeter) (m3)
Findes der en lettere måde?
Til sidst kan I diskutere og efterprøve, om det er muligt at lave en metode til at bestemme fastmassetallet uden, at alle stokke i stablen skal måles op (se nedenfor under baggrund).
Baggrund
Rummeter og kubikmeter fastmasse
En meget stor del af de effekter der produceres i skoven transporteres ud til bilfast vej, hvor det stables i stakke og sælges. Det bliver enten solgt i enheden rummeter (f.eks. brænde) – eller i enheden kubikmeter fastmasse (f.eks. gulvtræ).
Effekter af den slags kan være brænde, papirtræ, emballagetræ (træ til paller eller kasser), spånpladetræ, gulvtræ m.m.
For f.eks. papirtræ og gulvtræ gælder det, at de måles i rummeter og regnes om til kubikmeter fastmasse, inden de sælges. Da der ofte kan være tale om meget store træstakke, er det vigtigt at have en metode, hvor man kan fastsætte fastmassen, uden at man behøver at måle hver eneste stok.
Hvis ikke hver stok i stakken måles, er det nødvendigt at tage højde for flere faktorer som kan have betydning for mængden af luft i stakken og dermed fastmassetallet. Det kan være forhold som:
- Er træet stablet tæt eller løst
- Hvor stor er diameteren – små stokke giver lavere fastmassetal
- Hvor lige er træet – lige træ iver højere fastmassetal
- Hvor langt er træstokkene – langt træ giver lavere fastmassetal
- Hvor rent er stokkene skåret – sidder der gamle grene giver det et lavere fastmassetal.
Kan I finde på andre forhold?